Perkalian Vektor Matematika dan Contoh Soal

Dengan begitu, dapat kita pahami bahwa sifat perkalian vektor dengan skalar adalah distributif yang dapat dinyatakan k (A + B) = kA + kB

Baca juga: Pengertian, Rumus Dan Contoh Soal Dilatasi

2. Perkalian titik

Perkalian titik dapat kita sebut sebagai perkalian dot product yang menggunakan skalar sebagai hasil dari perkalian dua vektor dengan cosinus sudut apit kedua vektor tersebut. Misalnya, terdapat 2 vektor u dan v berikut.

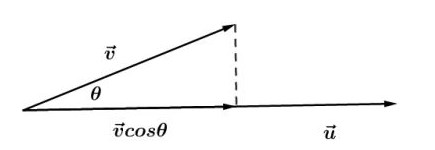
Perkalian titik dapat diartikan juga sebagai perkalian vektor u dengan komponen vektor v yang searah u. Dengan begitu, dapat kita tulis rumusnya seperti berikut.

Perkalian vektor antara dua titik buah dapat disimpulkan menghasilkan sebuah skalar. Perkalian titik ini dilambangkan dengan adanya lambang titik dengan hasil skalar sehingga dapat dikatakan sebagai perkalian skalar product juga.

Sifat perkalian titik dapat dikategorikan sebagai perkalian distributif dan komutatif dengan gambarannya sebagai berikut.

A (B + C) = A. B + A (Distributif)

A . B = B . A (Komutatif)

Baca juga: Rumus Pencerminan Terhadap Garis Y = min X

3. Perkalian silang

Perkalian silang pada dua buah vektor dapat diterapkan pada ruang tiga dimensi. Misalnya, u  = (u₁, u₂, u₃) dan v = (v₁, v₂, v₃). Hasil perkalian silang (cross product) dua vektor tersebut dituliskan sebagai berikut.

Keterangan:

u = vektor u

v = vektor v

u₁, u₂, u₃ : elemen-elemen vektor u

v₁, v₂, v₃ : elemen-elemen vektor v

Perkalian antara dua buah vektor dapat menggunakan metode perkalian silang yang dapat membentuk vektor pada bidang yang terbentuk oleh A dan B dengan arah yang tegak lurus. Dalam perkalian silang terdapat beberapa hal penting yang harus diperhatikan seperti berikut.

• Tidak berlaku perkalian silang dengan sifat komutatif. Maka persamaan A x B ≠ B x A.
• Berlaku perkalian silang dengan sifat anti komutatif. Maka persamaan A x B = -B x A.
• Vektor A tegak lurus dengan vektor B maka nilai α = 90⁰ dengan persamaan |A x B| = AB → sin 90⁰ = 1.
• Vektor A searah dengan vektor B maka nilai α = 0⁰ dengan persamaan |A x B| = 0 → sin 0⁰ = 0.
• Vektor A berlawanan arah dengan vektor B maka nilai α = 180⁰ dengan persamaan |A x B| = 0 → sin 180⁰ = 0.

Dengan begitu, dapat kita ambil kesimpulan bahwa perkalian vektor memiliki sifat anti komutatif, asosiatif, dan distributif. Hal ini dapat kita lihat pada gambaran berikut.

A × B ≠ B × A (Anti Komutatif)
k(A × B) = (kA) × B = A × (kB) (Asosiatif)
A × (B + C) = (A × B) + (A × C) (Distributif)
(A + B) × C = (A × C) + (B × C) (Distributif)

Baca juga: Rumus Pencerminan Terhadap Garis Y = X

Contoh soal

Setelah mempelajari pembahasan mengenai perkalian vektor matematika dan macam-macam jenis serta sifatnya, kalian dapat memahaminya lebih dalam berdasarkan soal-soal berikut.

1. Berikut diuraikan beberapa vektor.

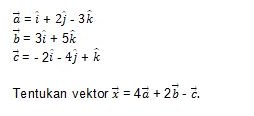
Pembahasan: