Perbedaan Simetri Lipat dan Simetri Putar

Perbedaan Simetri Lipat dan Simetri Putar – Bangun datar menjadi salah satu bagian dari materi geometri yang terbentuk melalui garis dan titik. Pada bangun datar sendiri, bangunan-bangunan yang termasuk di dalamnya merupakan jenis dua dimensi dengan ciri-ciri memiliki ukuran panjang dan lebar. Beberapa bangun datar memiliki perbedaan yang mencolok, seperti bentuk, ciri-ciri, dan sifat-sifatnya. Salah satu perbedaan yang terlihat pada sebuah bangun adalah mengenai aspek simetrinya.

Salah satu hal yang dapat membedakan bangun datar satu dengan yang lainnya adalah aspek simetri, yang terdiri atas simetri lipat dan putar. Namun, terdapat hal penting yang perlu dipahami bahwa tidak semua bangun datar memiliki aspek ini. Selain itu, terdapat pula bangun datar yang memiliki salah satu aspek saja seperti memiliki simetri lipat, tetapi tidak memiliki simetri putar dan begitu sebaliknya.

Baca juga: Simetri Lipat Bangun Datar pada Matematika

Baca juga: Simetri Putar Bangun Datar pada Matematika

Pada pembahasan kali ini, kalian akan mempelajari mengenai perbedaan yang terlihat pada sebuah bangun datar berdasarkan simetri lipat dan putarnya. Begitu penjelasannya.

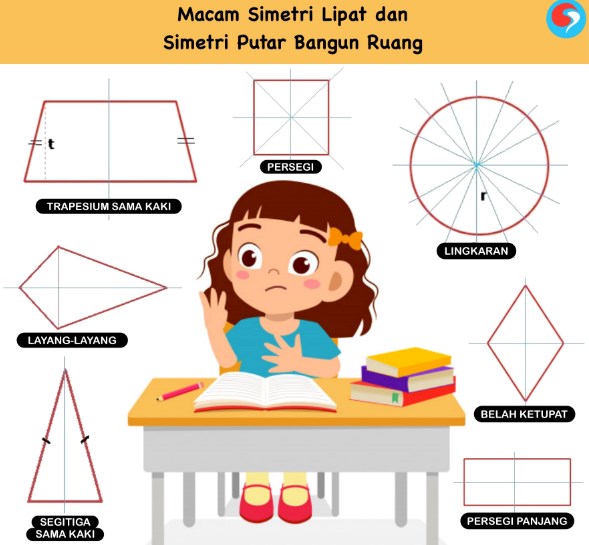
Simetri Lipat pada Bangun Datar

Simetri lipat dapat bermakna jumlah lipatan yang ada pada bangun datar. Lipatan ini dapat membagi bangun datar menjadi setengah bagian, seperempat bagian, hingga menutupi seluruh bangun datar yang dimaksud.

Dalam sebuah bangun datar yang dapat dibagi menjadi dua bagian yang sama besar berarti memiliki makna bahwa bangun datar tersebut mempunyai sebuah simetri lipat. Ketika mengetahui bangun datar tersebut memiliki simetri lipat, kalian dapat menemukan terlebih dahulu sumbu simetrinya. Sumbu simetri sendiri memiliki makna sebuah garis yang dapat membagi suatu bangun datar menjadi dua bagian yang sama besar.