2. Bilangan berpangkat negatif
Dengan adanya a tidak terdefinisikan dengan 0 maka bilangan a-n dengan n bilangan bulat positif merupakan bilangan berpangkat tak sebenarnya.
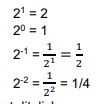
Contoh sederhana penerapan bilangan berpangkat dapat digunakan untuk mengukur sebuah satuan. Misalnya, seorang petani memiliki kebun berbentuk persegi dengan sisi kebun sepanjang 10 meter, jadi luas kebun adalah sisi x sisi = 10 x 10 atau 102 = 100 m2.
Sifat-Sifat Perpangkatan
Dalam perkalian berpangkat, sifat-sifat bilangannya berlaku seperti berikut.
1. Perkalian bilangan berpangkat
Sifatnya yang berlaku dengan rumus berikut am x an = am+n. Misalnya, 52 x 54 = (5 x 5) x (5 x 5 x 5 x 5) atau 52+4 = 56
2. Pembagian bilangan berpangkat
Sifat pembagian hampir sama dengan perkalian namun dalam pembagian pangkatnya harus dikurangi dengan rumus am : an = am-n. Misalnya, 67 x 64 = (6 : 6 : 6 : 6 : 6 : 6 : 6) x (6 : 6 : 6 : 6) atau 67-4 = 63
3. Sifat pemangkatan bilangan berpangkat
Sifatnya pemangkatan yang berlaku dengan rumus berikut (am)n = amxn. Misalnya, (52) 2 = 52 x 52 = (5 x 5) x (5 x 5) = 54
4. Sifat perpangkatan suatu perkalian atau pembagian
Apabila ada dua bilangan yang dikalikan dan dipangkatkan berlaku rumus (a x b)n = an x b n atau bilangan yang dibagi dengan rumus (a : b)n = an : b n. Misalnya,
(2p x q)3 = (2p) 3 x q3 = 8p3 x q3
Baca juga: Cara Menghitung Akar Kuadrat Secara Manual
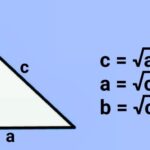
Pengertian Bilangan Bentuk Akar
Bilangan akar merupakan kebalikan dari bentuk pangkat dua. Misalnya, dalam mencari nilai dari bilangan a pada dasarnya adalah mencari suatu bilangan yang jika dipangkatkan n akan menghasilkan a. Dengan begitu, akar kuadrat menjadi invers atau operasi kebalikan dari akar bilangan pangkat.

Operasi Akar Bilangan
Operasi akar bilangan dapat menggunakan operasi penjumlahan dan pengurangan dan dapat disederhanakan dengan akar-akar yang memiliki pangkat sama.
Pada operasi perkalian dan pembagian, bagian yang dapat disederhanakan akar bilangan yang senama.
Misalnya, seperti berikut.

Dalam menghitung operasi akar, ingatlah bahwa bentuk akar tidak selalu memiliki nilai rasional. Hal ini dapat dilakukan pendekatan untuk bentuk akar menggunakan alat bantu seperti kalkulator, seperti = 1.4142. Bentuk akar yang non-rasional dapat diubah ke bentuk akar lain yang lebih sederhana dengan menggunakan operasi matematika.

Baca juga: Cara Menghitung Akar Pangkat 3 Dengan Benar
Rasional Bentuk Akar Kuadrat