Rumus Pencerminan Terhadap Garis Y = X

Rumus Pencerminan Terhadap Garis Y = X – Ilmu geometri sangatlah luas. Kita bisa mempelajarinya satu per satu, berikut rumus-rumus yang dipakai. Salah satu yang bisa kita pelajari adalah transformasi geometri. Melihat istilah tersebut mungkin kalian tidak terlalu kesulitan untuk mendefinisikannya dengan bahasa kalian sendiri.

Jadi transformasi geometri merupakan perubahan yang terjadi pada suatu bidang geometri, baik dari ukuran, posisi, ukuran, bentuk awal ke posisi, ataupun bentuk yang lainnya. Perubahan ini tidak sembarangan terjadi, melainkan terdapat aturan atau rumus tertentu yang membuat suatu objek mengalami perubahan.

Jika dilihat dari perubahannya, transformasi geometri bisa dibagi menjadi empat jenis. Antara lain pergeseran atau translasi, refleksi atau pencerminan, rotasi atau perputaran, dan perkalian atau dilatasi. Sebuah transformasi dapat dikatakan transformasi isometri apabila hasil perubahannya bersifat kongruen atau sama dan sebangun terhadap bidang yang ditransformasikan.

Baca juga: Pencerminan Terhadap Sumbu X Dan Sumbu Y

Transformasi isometri sendiri dapat dibagi lagi menjadi dua macam, yakni transformasi isometri berhadapan dan langsung. Rotasi atau translasi masuk dalam kategori transformasi isometri langsung. Sedangkan pencerminan atau refleksi merupakan transformasi isometri berhadapan.

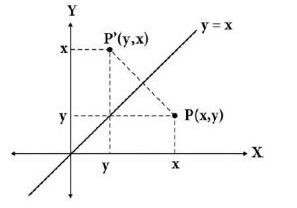
Dari kedua hal tersebut kita akan fokus membahas tentang pencerminan, khususnya pencerminan terhadap garis y=x. Kita mulai dari menjabarkan definisi dari pencerminan.

Definisi Pencerminan atau Refleksi

Pencerminan dalam materi transformasi geometri memiliki sifat yang serupa dengan cermin datar yang biasa kita pakai dalam kehidupan sehari-hari. Sehingga dapat dijelaskan bahwa pada pencerminan jarak antara satu titik dengan cermin akan sama dengan jarak bayangan dengan cermin.

Atau dapat diartikan bahwa pencerminan adalah transformasi geometri yang memindahkan seluruh titik pada suatu bidang geometri ke arah suatu garis yang menjadi cermin dengan jarak sejauh dua kali jarak titik-titik pada bidang geometri terhadap cermin.

Pencerminan ini mempunyai dua sifat utama. Pertama jarak titik ke cermin sama dengan jarak bayangan ke titik cermin. Sedangkan yang kedua bidang geometri yang dicerminkan akan sama persis dengan bayangannya.

Baca juga: Rumus Pencerminan Terhadap Garis Y = -X

Rumus Pencerminan Terhadap Garis Y = X

Pencerminan mempunyai beberapa jenis. Masing-masing jenis tersebut mempunyai matriks transformasi yang berbeda dan hal tersebut akan menentukan titik koordinat hasil pencerminan. Sebelumnya telah dibahas pencerminan terhadap sumbu x dan y. Sekarang kita bahas pencerminan terhadap garis y=x.

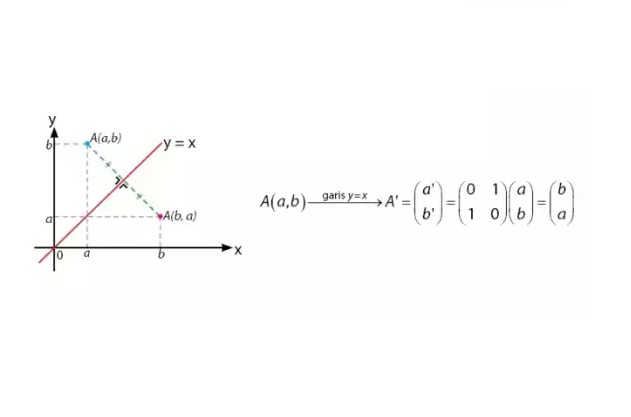
Pada pencerminan terhadap garis y=x, kita tulis matriks transformasi dan bayangan hasil pencerminan sebagai berikut.

Matriks transformasi:

|0  1|

|1  0|