Rumus Pencerminan Terhadap Garis Y = min X

Rumus Pencerminan Terhadap Garis Y = -X – Pada beberapa artikel sebelumnya kita sudah membahas mengenai transformasi geometri. Dan kalian tentu sudah tahu bahwa transformasi geometri merupakan bagian dari geometri yang berhubungan dengan perubahan, baik perubahan bentuk penyajian maupun perubahan letak.  Dapat diartikan bahwa transformasi geometri adalah suatu cara mengubah setiap koordinat titik menjadi koordinat lainnya dengan aturan tertentu.

Dalam bangun geometri kita mengenal ada banyak bangun ruang. Dan seluruh bangun ruang itu terdiri dari garis-garis yang dihubungkan secara sistematis. Sedangkan garis sendiri merupakan kumpulan titik yang dihubungkan satu sama lain. Maka dari itu transformasi geometri ini berlaku pada bangun ruang maupun titik-titik dan garis-garis.

Transformasi atau perubahan pada geometri bisa dilakukan dalam empat cara. Yaitu perputaran, pergeseran, perbesaran atau pengecilan, dan pencerminan. Pada artikel ini kita bahas mengenai pencerminan, khususnya pencerminan terhadap garis y=-x.

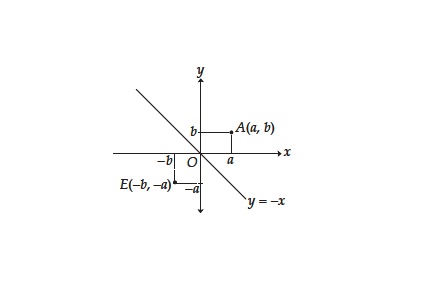
Seperti yang sudah dibahas pada kesempatan sebelumnya, pencerminan dalam geometri mempunyai sifat yang sama persis dengan cermin yang biasa digunakan untuk berkaca. Artinya dalam pencerminan geometri objek dan bayangannya mempunyai bentuk dan ukuran yang sama. Selain itu jarak setiap titik pada objek ke cermin juga sama dengan jarak antara setiap titik pada bayangan ke cermin.

Tidak hanya itu, tinggi bayangan dan objek juga sama persis. Termasuk garis yang menghubungkan titik pada objek dengan titik pada bayangan. Keduanya selalu tegak lurus terhadap cermin.

Baca juga: Rumus Pencerminan Terhadap Garis Y = X

Rumus Pencerminan Terhadap Garis Y=-x

Sekarang kita masuk ke pembahasan inti. Ketika berbicara soal pencerminan maka tidak akan terlepas dari yang namanya koordinat kartesius. Pada koordinat kartesius suatu titik atau persamaan bisa diubah secara geometri, termasuk lewat pencerminan.

Pencerminan terhadap garis y=-x pada dasarnya mengubah posisi objek pada koordinat kartesius. Caranya adalah dengan mencerminkan objek tersebut terhadap garis y=-x. Simak gambar di bawah ini untuk lebih jelasnya.

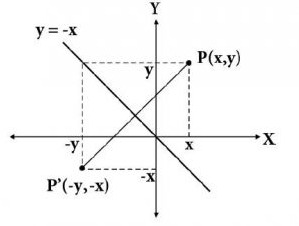
Dilihat dari contoh di atas kita bisa mengetahui titik P dengan koordinat (x, y) dicerminkan terhadap garis y=-x. Dari pencerminan tersebut kita peroleh hasil bayangan titik P adalah titik P’ dengan koordinat (-y, -x). Selain digambarkan dengan koordinat kartesius, kita juga bisa menuliskan hasil pencerminan tersebut dalam bentuk matriks. Berikut penulisan matriks dari contoh di atas:

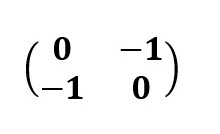
Sedangkan matriks dari bayangan hasil transformasinya adalah:

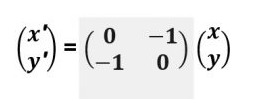
Matriks transformasi itu berlaku untuk koordinat suatu titik dan persamaan garis atau kurva. Hasil pencerminannya adalah sebagai berikut: