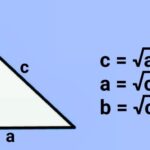
Rumus Identitas Trigonometri – Mungkin sebagian besar dari Anda sudah tidak asing lagi jika mendengar kata trigonometri. Trigonometri merupakan sebuah ilmu matematika yang mempelajari tentang hubungan antara sudut dengan sisi yang ada dalam bangun datar segitiga.
Ada banyak sekali rumus yang akan kita jumpai saat mempelajari trigonometri. Beberapa diantaranya adalah limit trigonometri, identitas , persamaan trigonometri dan lain sebagainya. Namun pada kesempatan kali ini kami hanya akan membahas mengenai identitas trigonometri.

Pada awalnya mungkin Anda akan mengalami kesulitan untuk memahami materi identitas trigonometri. Namun sebenarnya materi mengenai identitas trigonometri ini sangat mudah untuk dipahami dengan syarat Anda harus mengerti konsep dasarnya.
Maka dari itu, pada pembahasan kali ini kami akan mengulas secara lengkap mengenai identitas trigonometri mulai dari pengertian trigonometri, pengertian trigonometri, rumus-rumus, sampai dengan contoh soalnya sehingga akan memudahkan Anda untuk mempelajarinya.
Pengertian Trigonometri
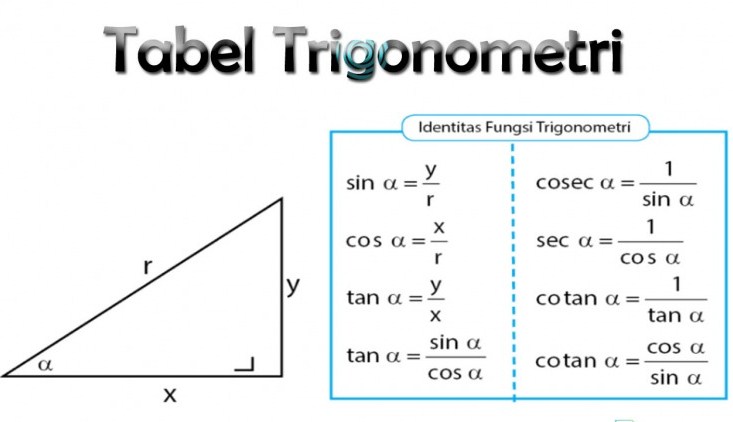
Seperti yang sudah kami jelaskan diatas bahwa pengertian trigonometri adalah salah satu cabang ilmu matematika yang mempelajari mengenai hubungan antara sisi dengan sudut dari sebuah bangun datar segitiga dan fungsi dasar yang muncul dari relasi tersebut.
Trigonometri sendiri sangat identik dengan fungsi trigonometri yang mencakup sinus (sin), cosinus (cos), tangen (tan), cosecan (cosec), secan (sec) dan juga cotangen. Semua fungsi tersebut merupakan cara yang digunakan untuk dapat menentukan suatu sisi sebuah bangun segitiga dan juga sudut yang telah terbentuk dari sisi dalam bangun datar segitiga.