Pengertian, Rumus Dan Contoh Soal Dilatasi

Pengertian Dan Rumus Dilatasi – Sebelumnya kita telah membahas transformasi geometri bangun datar, khususnya mengenai translasi. Pada kesempatan ini kita bahas mengenai dilatasi. Tujuannya untuk memperdalam pemahaman mengenai transformasi dilatasi. Sebab materi ini masih bisa dibahas lebih detail.

Sekilas tentang Dilatasi

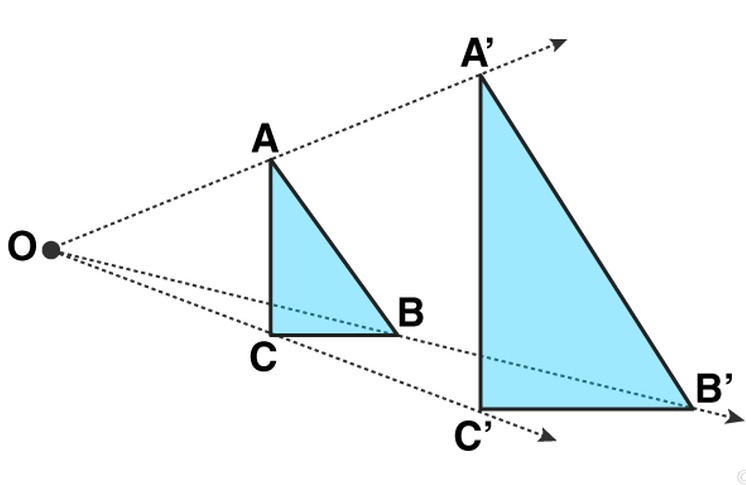
Sebelumnya kalian mungkin sudah membaca bahwa dilatasi merupakan transformasi geometri yang dilakukan dengan mengubah ukuran suatu bangun dengan cara memperbesar maupun memperkecil, namun tidak mengubah bentuk bangun datar tersebut. Di samping itu dilatasi juga bisa diartikan sebagai transformasi yang memindahkan suatu titik pada bangun geometri yang bergantung pada titik pusat dilatasi dan faktor skala dilatasi. Sehingga bayangan dari bangun geometri yang didilatasikan berubah ukuran, baik membesar maupun mengecil.

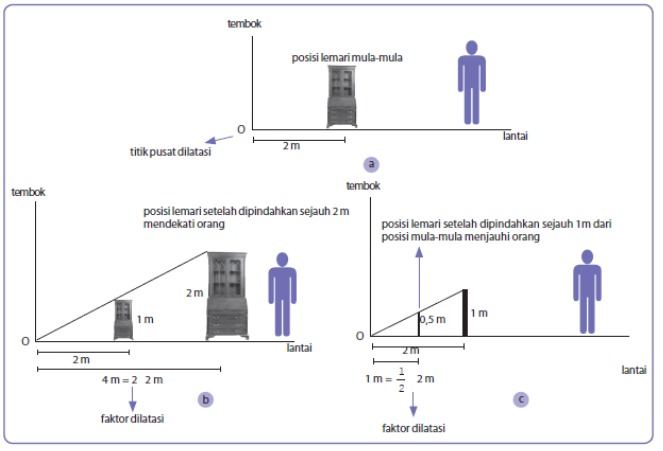
Mungkin kalian masih bingung dengan penjelasan di atas. Contohnya bayangkan objek yang didilatasi merupakan sebuah truk yang melaju ke arah kita. Jika dilihat dari jauh truk tersebut akan terlihat kecil. Akan tetapi saat semakin dekat truk akan terlihat semakin besar. Hal inilah yang dinamakan dilatasi. Di samping itu dilatasi juga bisa dianalogikan dengan mendekatkan objek ataupun menjauhkan objek dari kita. Simak contoh berikut sebagai gambaran.

Baca juga: Rumus Dan Contoh Soal Translasi

Penerapan dilatasi dalam kehidupan sehari-hari tidaklah sulit untuk dijumpai. Misalnya adalah ukuran pas foto dari 2 x 3, 3 x 4, hingga 4 x 6. Ini merupakan salah satu penerapan transformasi geometri dilatasi.

Contoh lainnya adalah miniatur atau mainan yang merupakan replika dari barang yang lebih besar dengan skala yang sesuai. Ataupun map hingga atlas yang ukurannya berbeda-beda namun jika dihitung lebih dalam semuanya akan menunjukkan jarak atau luas yang sama.

Dilatasi bisa ditentukan dengan menganalisis titik pusat dan faktor dilatasi. Transformasi perubahan ukuran ini ditentukan berdasarkan titik pusat dilatasi dan faktor dilatasi yang sudah disebutkan sebelumnya. Di mana notasinya adalah O (0, 0) untuk titik pusat dan k (O, k) untuk faktor skala. Sebagai tambahan, titik dilatasi merupakan suatu titik yang bisa menentukan posisi dilatasi yang mana menjadi poin pertemuan dari seluruh garis lurus.

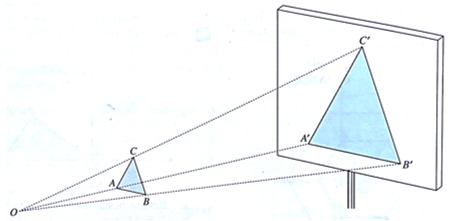
Di sisi lain garis lurus tersebut saling menghubungkan titik-titik dalam suatu bentuk. Dengan kata lain hal tersebut menjadi hasil dari titik dilatasi. Lalu apa yang dimaksud dengan faktor dilatasi?

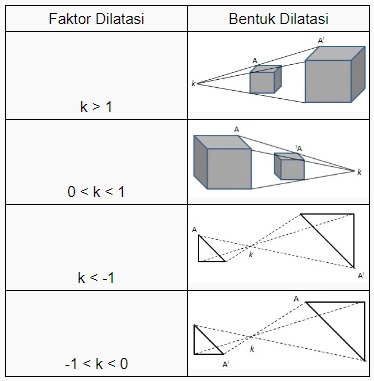
Faktor dilatasi adalah faktor perkalian maupun multiplikasi dari struktur-struktur bangun geometri yang sudah mengalami dilatasi. Dari faktor tersebut kita bisa mengetahui seberapa besar hasil yang ditunjukkan. Kemudian diperluas menjadi bentuk geometris dan dilambangkan dengan huruf k. Apabila k > 1 atau K < -1 maka bisa ditarik kesimpulan bahwa hasil pelebaran lebih besar dari geometri itu sendiri.

Perlu diingat, dilatasi bisa ditulis dengan format sebagai berikut:

(D, k) = (Titik dilatasi, faktor dilatasi)

Sedangkan konsep dilatasi bisa dilihat pada tabel berikut:

Baca juga: Rumus Kesebangunan Bangun Datar

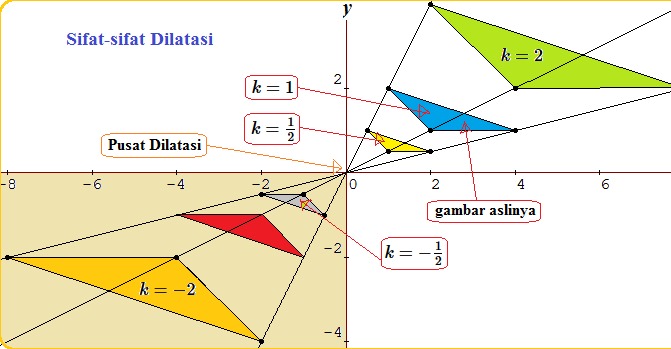
Sifat Dilatasi

Beberapa macam transformasi geometri yang kita ketahui memiliki ciri khusus yang membuatnya mudah untuk dibedakan dengan jenis lainnya. Pada dilatasi, apabila yang mengalami dilatasi merupakan suatu bangun, untuk pusat dilatasi maka dilatasinya akan mengubah bentuk geometri tersebut secara otomatis. Sebagai gambaran (P, k) adalah notasi dari dilatasi dengan pusat di P.

D[(0,0),k]

A(x,y)——————>A’ (kx, ky)