Nilai Sin Cos Tan 53 dan 37 Derajat – Cabang ilmu matematika yang membahas mengenai sudut biasanya berhubungan dengan trigonometri. Trigonometri sendiri membahas mengenai sudut yang berhubungan dengan panjang pada sebuah segitiga. Biasanya, trigonometri akan dikaitkan dengan bidang datar segitiga siku-siku yang memiliki sudut lancip dan sudut siku-siku. Jika salah satu satu sudut 90 derajat dan sudut lainnya diketahui, menjadikan sudut ketiga dapat ditemukan karena tiga sudut segitiga apabila dijumlahkan menjadi 180 derajat.
Hubungan antara panjang dan sudut segitiga dapat didefinisikan berdasarkan sisi-sisinya. Segitiga memiliki tiga sisi, yaitu sisi samping yang letaknya menempel atau letaknya disamping, sisi depan yang letaknya berhadapan dengan sudut yang ditinjau, dan sisi miring yang posisinya miring. Dengan begitu, dalam segitiga memiliki sudut trigonometri dengan rumus dasarnya, yaitu cos, sin, dan tan. Rumus ini dapat didapat dari sisi-sisi segitiga bahwa sin didapat dari sisi depan per sisi miring, cos didapat dari sisi samping per sisi miring, dan tan didapat dari sisi depan per sisi miring.
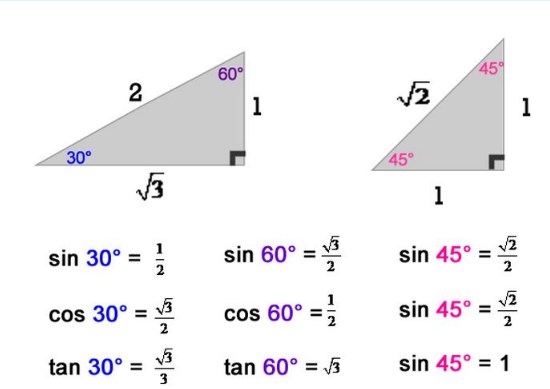
Baca juga: Pengurangan dan Penjumlahan Vektor Beserta Contoh Soal





