Contoh Soal Kuartil Data Tunggal dan Data Kelompok

Kuartil Data Tunggal dan Data Kelompok – Data kuartil umumnya memiliki terdiri atas macam bentuk data, yaitu data tunggal dan data kelompok. Biasanya, tidak ada perbedaan mendasar dari penggunaan data tunggal dan kelompok, baik dari rumus jangkauan, antarkuartil, simpangan kuartil, atau langkah-langkahnya.

Kuartil umumnya adalah nilai-nilai yang terbagi atas data yang diurutkan ke dalam empat bagian yang sama besar. Simbol dari kuartil adalah Q dan terdiri atas tiga bagian, yaitu kuartil atas, tengah, dan bawah.

Baca juga: Cara Mencari Mean, Modus, Dan Median

Hanya saja, terdapat perbedaan mendasar antara data tunggal dan data kelompok. Hal ini dapat dilihat dari penggunaan datanya biasanya dapat lebih terlihat di data tunggal bagian mana yang terkecil hingga terbesar. Lalu, pada data kelompok data terkecil dan data terbesarnya diambil dari batas bawah dan batas atasnya.

Dalam menentukan data tunggal dan kelompok, terdapat beberapa catatan dalam mengolah data sebagai berikut.

1. Pada suatu kumpulan data, setiap data yang ada dapat ditambah dan dikurangi.]
2. Pada data yang nilai statistiknya berubah meliputi rata-rata, median, modus dan kuartil, sedangkan data yang nilai statistiknya tidak berubah meliputi jangkauan, simpangan kuartil, dan simpangan baku.
3. Pada suatu kumpulan data akan dibagi dengan suatu bilangan yang menjadikan nilai statistiknya berubah.

Perlu diingat kembali, data tunggal dan kelompok hadir pada simpangan kuartil yang dapat disebut jangkauan semi antarkuartil dan berikut adalah rumusnya.

Baca juga: Cara Menghitung Simpangan Baku

Kuartil Data Tunggal

Dalam menentukan kuartil data tunggal, kita harus mempertimbangkan berapa data yang hadir dan disimbolkan dengan n. Pertimbangan ini dapat membantu dalam penghitungan yang dasarnya adalah kondisi dari banyaknya data.

Misalnya, terdapat data berikut.

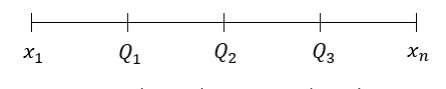
Data kuartil di atas dapat menentukan kondisi banyaknya data seperti berikut.

Pada rumus di atas telah menjelaskan beberapa cara dalam menentukan data tunggal dengan jumlah data yang ada. Pada jumlah data dengan jumlah kecil dapat ditentukan dengan lebih mudah berdasarkan piramida berikut.

Baca juga: Tabel Distribusi Frekuensi Data Tunggal Dan Kelompok

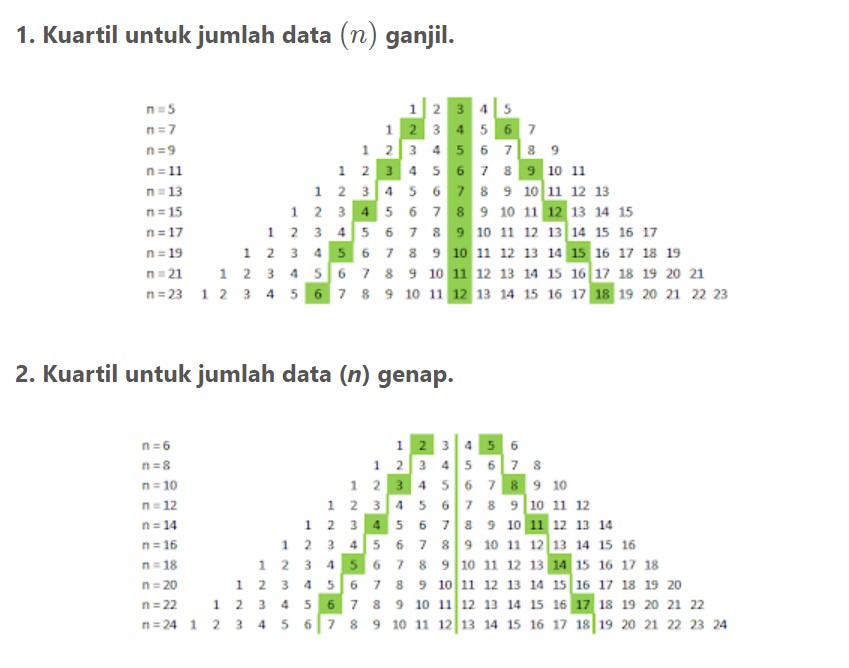
Piramida di atas menjelaskan mengenai letak kuartil dengan dua nilai. Nilai kuartil dapat berupa rata-rata dari kedua nilai yang dijelaskan. Agar lebih memahami mengenai data kuartil tunggal, berikut soal-soal yang dapat dipelajari lebih lanjut.

1. Berikut adalah data panjang jalan di daerah x, yaitu 5 6 7 3 2. Kuartil dari data panjang tersebut adalah ….

A. 5

B. 6

C. 6,5

D. 7,5

2. Dalam sebuah kelas, terdapat sebuah data untuk mengukur tinggi badan siswanya. Hasil dan sampel tersebut membutuhkan 10 siswa tertinggi di kelas. Data kesepuluh siswa tersebut, yaitu 172, 167, 180, 171, 169, 160, 175, 173, 170. Nilai kuartil dari data tinggi kesepuluh siswa tersebut adalah ….

A. 172

B. 173